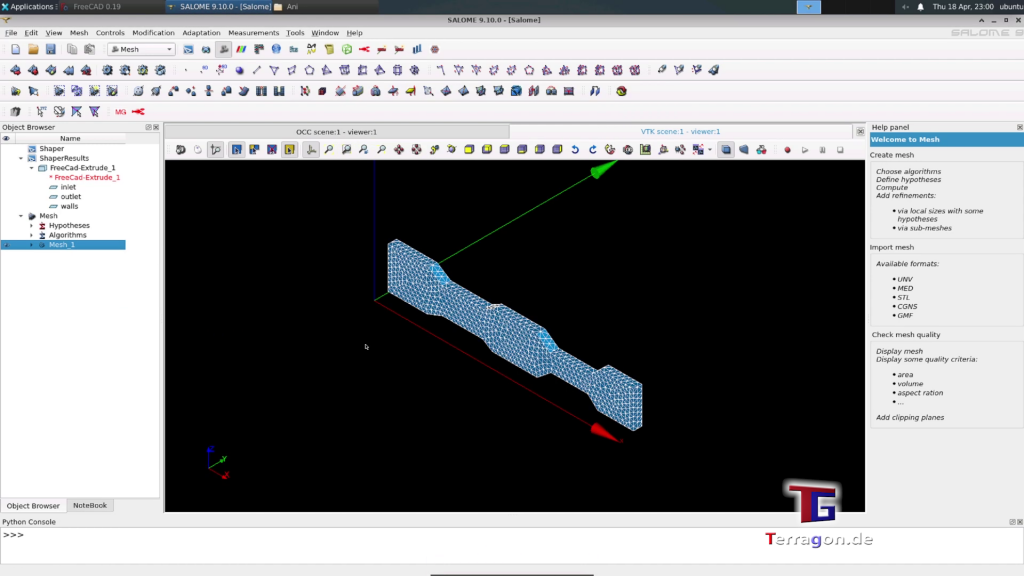
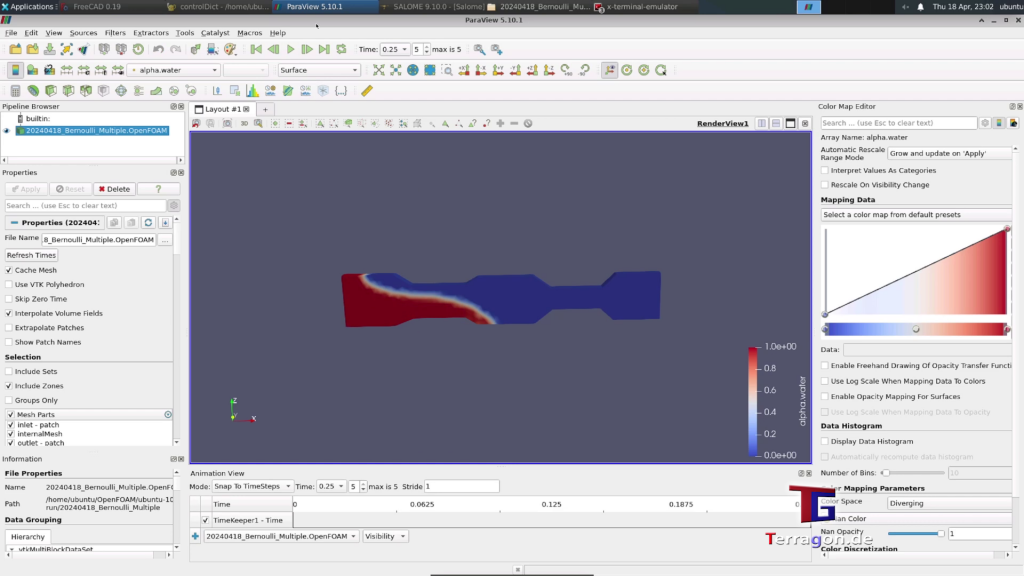
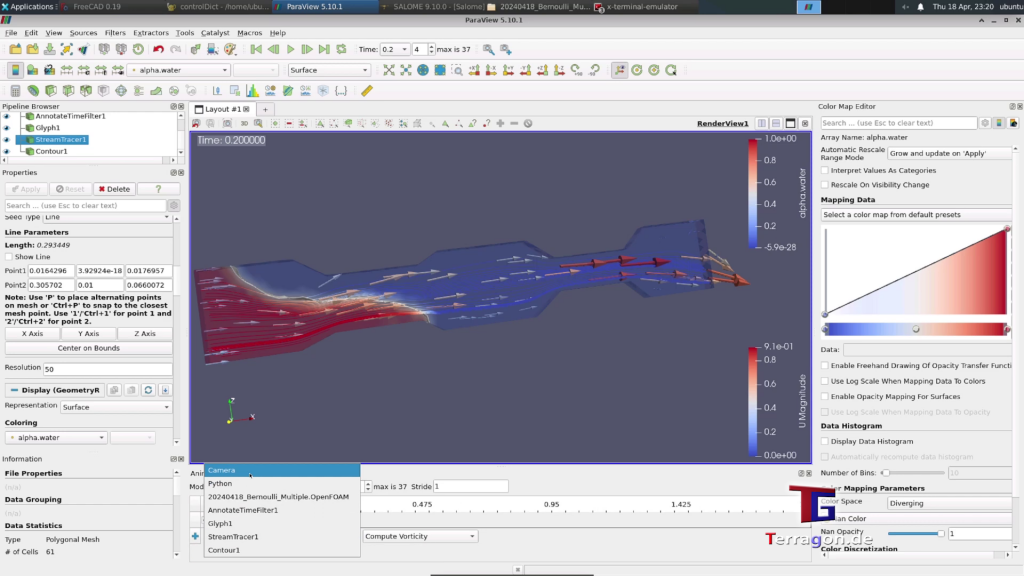
Ladies and gentlemen, esteemed colleagues, and curious minds,

Today, we delve into the intricate realm of fluid dynamics, guided by the profound wisdom encapsulated within Bernoulli’s principle. Allow me to elucidate the essence of this fundamental concept that orchestrates the dance of fluids in our universe.

At its core, Bernoulli’s principle unveils the intimate relationship between pressure, speed, and height within a fluid medium. Conceived by the brilliant mind of Daniel Bernoulli and refined by the scholarly prowess of Leonhard Euler, this principle serves as a beacon illuminating the behavior of fluids since its inception in 1738.

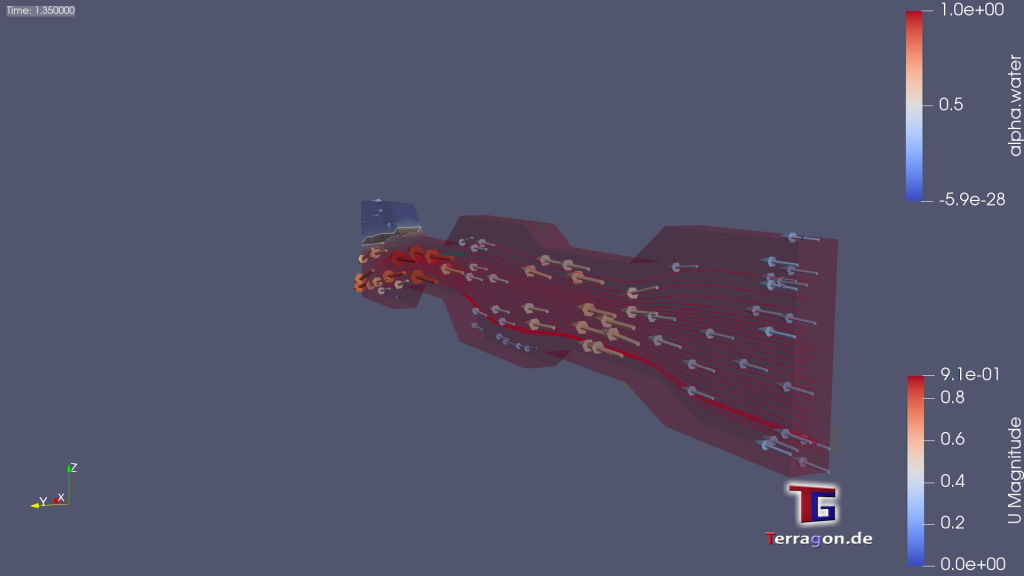
Picture a river flowing gracefully, its waters whispering secrets of energy conservation. Indeed, Bernoulli’s principle emerges from the hallowed halls of energy conservation, proclaiming that within a steady flow, the total energy of a fluid remains constant. As the fluid traverses its path, kinetic energy surges with the swiftness of its motion, while potential and internal energies ebb in synchrony, yielding to the fluid’s momentum.

In the symphony of motion, Newton’s timeless laws also lend their wisdom to Bernoulli’s principle. When a fluid volume traverses from regions of disparate pressure, Newton’s second law heralds a net force, propelling the fluid along its designated course. Thus, within the tapestry of fluid flow, pressure differentials sculpt the landscape, dictating the pace of particles as they navigate through space and time.

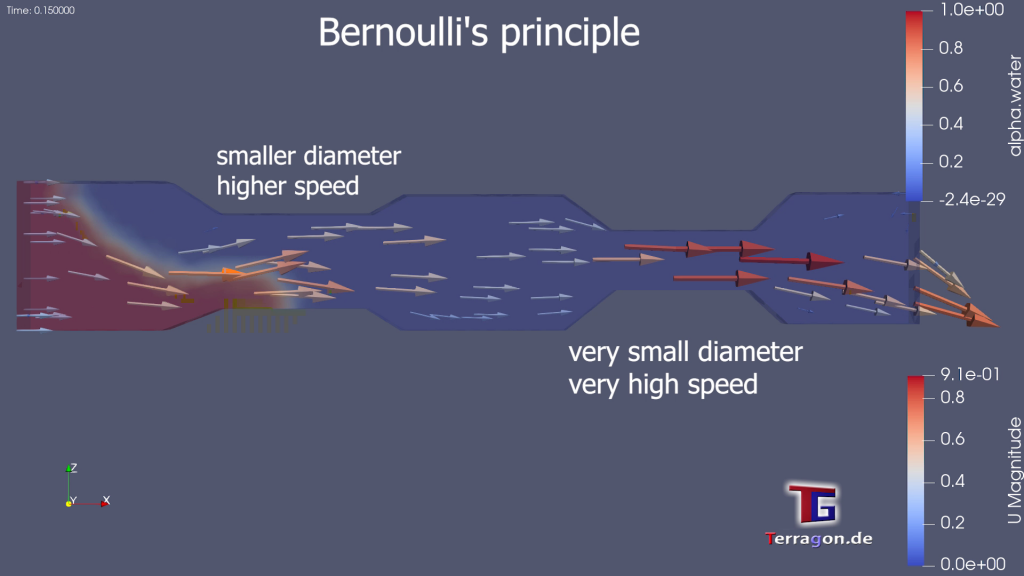
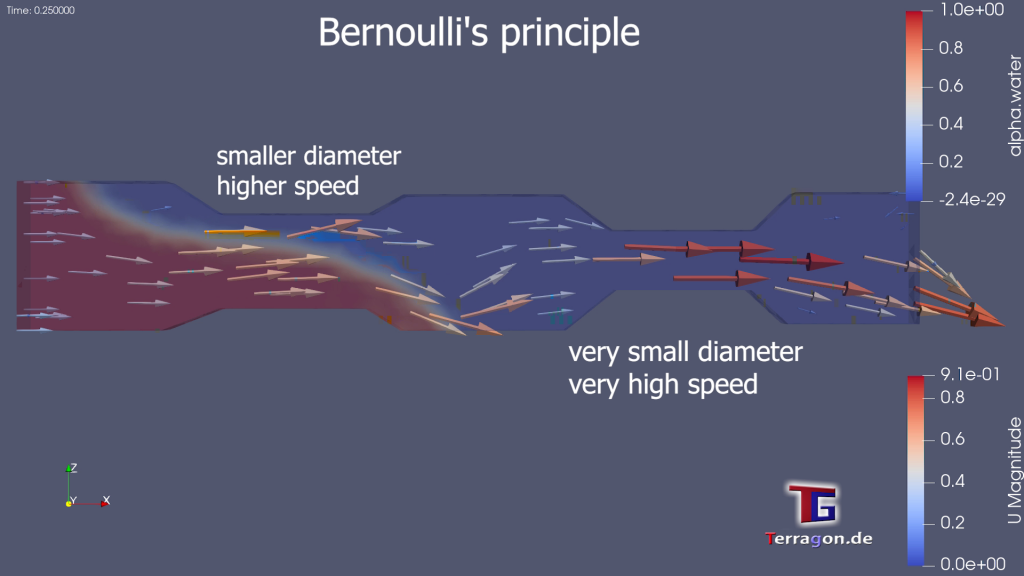
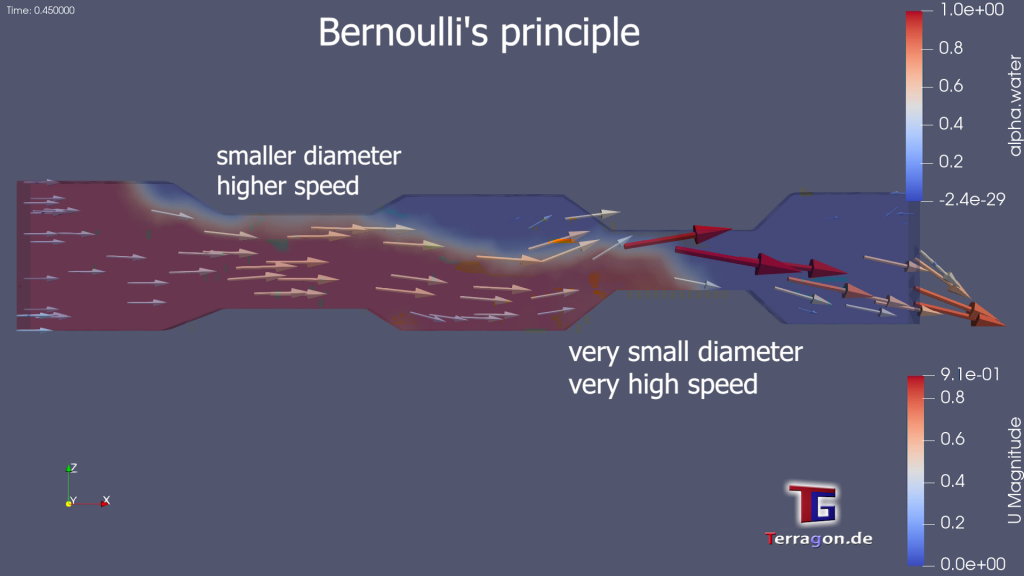
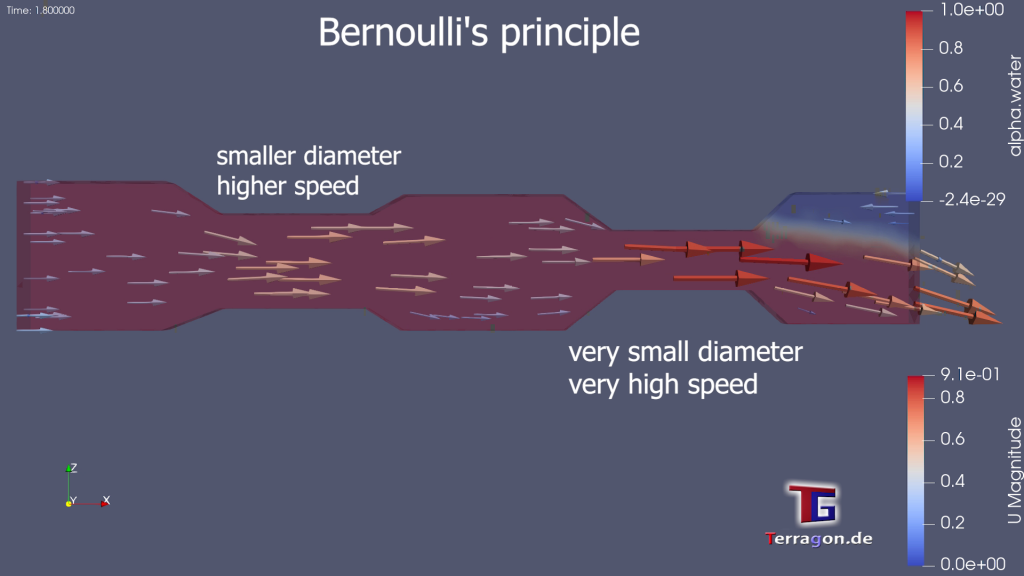
Imagine, if you will, a river’s gentle current, where speed and pressure intertwine in a delicate ballet. As the fluid cascades from regions of high to low pressure, its velocity crescendos, mirroring the inverse relationship between pressure and speed. This elegant choreography unfolds, revealing that the zenith of speed resides in the realm of minimal pressure, while the nadir emerges amidst the embrace of heightened pressure.

Yet, let us not forget the constraints that bind Bernoulli’s principle within the confines of isentropic flows. In the realm of fluid dynamics, where turbulence reigns and thermal energies dance, Bernoulli’s principle finds solace solely in the realms of reversible and adiabatic processes. Within these bounds, its wisdom manifests in various incarnations, from the simplicity of incompressible flows to the complexity of compressible phenomena at higher Mach numbers.

In closing, let us cherish the legacy of Bernoulli’s principle—a testament to the ingenuity of those who unravel the mysteries of nature. As we embark on our journey through the labyrinth of fluid dynamics, may we heed its teachings, for within its hallowed halls lie the keys to understanding the symphony of motion that permeates our universe.

Thank you.

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

•